DT                   T a m á s  D é n e s mathematician                                       TD

free-lance expert

 

e-mail: tdenest@freemail.hu

 

 

 


 Komplementer prímszita

 és alkalmazása a prímszámok számának becslésére

 

 

 

 

ABSTRACT

A címbeli komplementer kifejezés azt jelzi, hogy a szokásossal ellentétes megközelítést követünk, azaz

 
 direkt képletet, szükséges és elegendő feltételt adunk meg az összes 6k+1 és  6k-1 alakú összetett számokra, az így előállított táblázat  pontosan a prímszámokat nem tartalmazza, azaz a komplementer táblázatban találhatók meg az összes prímszámok, ezt nevezzük  komplementer prímszitának.

A  komplementer prímszita módszer lehetőséget nyújt a prímszámok előállítására faktorizáció nélkül,

ugyanakkor a konstruktív bizonyításból  adódik az összetett számok kéttényezős felbontása.

Eljárásunk alkalmas a természetes számok bármely  (m,n)  intervallumába eső összes  prímszámok előállítására, valamint az x-nél kisebb prímszámok számának -nek  becslésére.

 

1.Tétel

 

Minden 3-nál nagyobb  p  prímszám  6k+1 vagy  6k-1  alakú,  ahol  k = 1,2,3,... természetes szám.

 

Bizonyítás:

 

Tegyük fel, hogy  p  prím, de nem  6k+1 vagy  6k-1  alakú. Ekkor csak a következő esetek állhatnak elő

 

(1.1)                  p= 6k+2    vagy   p= 6k-2      ez páros, így nem lehet prím.

 

(1.2)                  p= 6k+3    vagy   p= 6k-3      ez osztható  3-al, így nem lehet prím.

 

(1.3)                  p= 6k+4    vagy   p= 6k-4      ez páros, így nem lehet prím.

 

(1.4)                  p= 6k+5    vagy   p= 6k-5         p= 6k+5 = 6(k+1)-1  vagy  

                                                                              p= 6k-5 = 6(k-1)+1  ezek              

                                                                              viszont a feltételezett alakúak.

                                                                                                                  Q.E.D.

 

 

 

 

 

Az  1.tétel  alapján tehát, ha a természetes számokat  az alábbi módon rendezzük hat oszlopba (lásd  1.tábla), akkor az összes prímszám az  1.  és az  5. oszlopban helyezkedik el.  Méghozzá az 1.oszlopban a  6k+1, míg az  5.oszlopban  a  6k-1  alakúak.

 

 

 

                                                                                      1.Tábla

 

                                                         6k+1                                                 6k-1

                                                                                                                  

                                             1          2           3        4        5       6

                                             7          8           9      10      11      12

                                           13        14         15      16      17      18

                                           19        20         21      22      23      24

                                           25        26         27      28      29      30

                                           31        32         33      34      35      36

                                          37         38         39      40      41      42

                                          43         44         45      46      47      48

                                          49         50         51      52      53      54

                                          55         56         57      58      59      60

                                          61         62         63      64      65      66

                                          67         68         69      70      71      72

                                          73         74         75      76      77      78

                                          79         80         81      82      83      84

                                          85         86         87      88      89      90

                                          91         92         93      94      95      96

                                          97         98         99    100    101     102

                                          . . . .

 

Az  1.tételből rögtön adódik  egy gyors felsőkorlát az  N-nél kisebb prímszámok számára:

 

(1.5)                                              

 

Az  1.tétel  alapján a 3-nál nagyobb prímszámok szempontjából elegendő csupán a   alakú természetes számokat vizsgálni. Az alábbi  2.tétel  szükséges és elegendő feltételt ad a  alakú összetett számokra, azaz a  komplementer prímszitára.

 

2.Tétel  (Komplementer prímszita)

 

Legyenek  N, k, u, v  természetes számok, valamint  u,v 1.

N= 6k+1  akkor és csak akkor összetett szám, ha   k =  6uv + u + v     vagy    k= 6uv - u - v   

N= 6k -1  akkor és csak akkor összetett szám, ha   k =  6uv -  u + v     vagy    k= 6uv +u - v   

 

 

Bizonyítás  (szükségesség):

 

Ha  N= 6k+1  összetett szám, akkor  6k+1 = dr   k=

 

Ez két esetben lehetséges:

 

(2.1)     d= 6u+1  és        r= 6v+1 

 

              k= ==  6uv + u + v

 

 

 

(2.2)     d= 6u-1  és      r= 6v-1

 

              k= = = 6uv -u -v

 

 

Ha  N= 6k-1  összetett szám, akkor  6k-1= dr   k=

 

Ez két esetben lehetséges:

 

(2.3)             d= 6u+1   és       r= 6v-1  

            k=  =  =  6uv -u + v

 

Mivel ez az összefüggés u, v-re szimmetrikus, így a másik megoldás 

 

(2.4)          k= 6uv + u - v

 

Ezzel a tétel szükséges ágát bebizonyítottuk.

 

 

Bizonyítás  (elégségesség):

 

Legyen   k= 6uv+u+v  és  N= 6k+1, valamint   v=u+r ,  ahol    , ekkor

 

(2.5)          N=6(6u(u+r)+u+u+r)+1 = 6(6+6ur+2u+r)+1 = =

                  ==  (6u+1)(6v+1)    ez nyilvánvalóan nem prím.

 

 

 

Legyen  k= 6uv-u-v   és  N= 6k+1, valamint  v=u+r,  ahol   , ekkor

 

(2.6)         N=6(6u(u+r)-u-(u+r))+1 = 6(6+6ur-2u-r)+1 = =

                 ==  (6u-1)(6v-1)   ez nyilvánvalóan nem prím.

 

 

Legyen  k=6uv-u+v   és  N= 6k-1, valamint  v=u+r,  ahol    , ekkor

 

(2.7)           N=6(6u(u+r)-u+u+r)-1 = 6(6+6ur+r)-1 = =

                   =(6u+1)(6u-1)+6r(6u+1) = (6u+1)(6u-1+6r) =  (6u+1)(6v-1)    ez nyilvánvalóan nem prím.

 

 

Legyen  k=6uv+u-v   és   N=6k-1, valamint  v=u+r,  ahol    , ekkor

 

(2.8)          N=6(6u(u+r)+u-(u+r))-1 = 6(6+6ur-r)-1 = =

                  =(6u+1)(6u-1)+6r(6u-1) = (6u-1)(6u+1+6r) =  (6u-1)(6v+1)     ez nyilvánvalóan nem prím.

         

Q.E.D.

 

Következmények:

 

K2.1.  A (2.5) - (2.8) levezetések megadják bármely  alakú  N  természetes szám  egy  szorzattá

            bontását is.   Ha 6u-1, 6u+1, 6v-1, 6v+1  prímek (ami az 1.tétel szerint lehetséges), akkor ponto-

            san az  N szám  prímfelbontását kapjuk.

 

         Ha bevezetjük  az   a=6u+1   és   b=6u-1   jelöléseket, akkor tehát  minden    alakú

         természetes szám felírható az alábbi négy alak valamelyikeként:

 

(2.9)                                     

 

         Példa :      u=23,  r=29   a=139,  b=137     = 139x313= 43507   = 137x311= 42607 

                                                                                            = 139x311= 43229   = 137x313= 42881                             

 

 

K2.2.  Mivel  a  K2.1.-ben bevezetett jelölések szerint  mindig teljesül, így a  (2.9)-beli     (i=1,2,3,4)

            kifejezések soha nem egyenlőek, kivéve azt az egy esetet, mikor  r=0

            Ha megvizsgáljuk az    számok nagyságviszonyait, a  2.tábla  relációs mátrixát kapjuk.

 

                tehát   

                tehát    

                tehát    

                tehát    

                tehát    

             tehát    

 

 

                                                      

 

                                         2.Tábla

 

                                                                  

                                                    -                  

                                                          -           

                                                               -     

                                                                   -

 

          

 

Tehát   mindig fennáll  az         reláció.

 

Az  1. és 2.tételből adódik egy igen egyszerű bizonyítás a prímszámok végtelenségére:

 

Tétel

Végtelen sok prímszám van.

 

Bizonyítás (indirekt):

Az  1.tétel alapján elegendő csak a    alakú  természetes számokat vizsgálni.

Tegyük fel, hogy  véges sok prímszám van, és ezek közül  P=6K+1 az utolsó  6k+1 alakú prímszám.  Ekkor minden    természetes szám összetett.

Így  a  2.tétel  szerint  p prímtényezős felbontása az alábbi:      ahol   minden       és    prím.

A feltételezés szerint  a prímtényezős felbontásban mindegyik    ebből következik, hogy

                                                             

Ez azt jelenti, hogy a    alakú számok száma véges, ami nem igaz, tehát nincs ilyen  K, azaz a  6k+1 alakú prímszámok száma végtelen. A levezetés hasonlóan végezhető  a 

6k-1 alakú prímszámokra is.

                                                                                                                                                                 Q.E.D.

 

K2.3.

 

A  (2.5) - (2.8)  levezetések alapján vizsgáljuk egy tetszőleges  N természetes számig az összes  6k+1 és  6k-1 alakú összetett (nem prím) számok számát. Azaz vizsgáljuk az   (i= 1,2,3,4) egyenlőtlenségeket.

 

 

(2.10)      (6u+1)(6u+1+6r)    

 

 

(2.11)   

 

 

(2.12)      (6u-1)(6u-1+6r)     

 

(2.13)    

 

 

(2.14)       (6u+1)(6u-1+6r)      

 

(2.15)    

 

 

(2.16)        (6u-1)(6u+1+6r)      

 

(2.17)    

 

 

Mivel az  u,v  paraméter párok az    (i=1,2,3,4)   kifejezésekben szimmetrikusak, így nyilvánvaló, hogy csak az   , azaz az   esetekre kell az    értékeket előállítani ahhoz, hogy N-ig az összes  6k+1 és  6k-1  alakú összetett számok legalább egyszer előálljanak.  Ebből következnek az alábbi összefüggések:

 

 

(2.18)       tehát  

 

 

(2.19)       tehát  

 

 

(2.20)       tehát  

 

 

 

 

Vezessük be a    jelölést, amely az  összes    típusú összetett számok előállításához elegendő u,v  párok számát jelöli.

 

(2.21)                      

 

(2.22)                    

 

(2.23)                     

 

(2.24)                     

 

 

(2.25)                

 

 

A  fenti  levezetés csupán az elegendőséget biztosítja, azaz  az összes különböző  u,v  párok előállítását. Ez viszont megengedi, hogy az előállítás során bizonyos  összetett számok többször forduljanak elő, így     annyival nagyobb az  N-ig előforduló összes  6k+1 és 6k-1 alakú összetett számok számánál  (jele: ), amennyi ezeknek a többszörös multiplicitással szereplő elemeknek a száma  (jele:  m(N)), azaz

 

(2.26)                

 

Ha  KP(N)-nel jelöljük az általunk javasolt  komplementer prímszita eljárással előállított prímszámok számát, akkor adódik, hogy

 

(2.27)                  KP(N) =  

 

A fenti levezetések alapján  K(N) értékét pontosan meghatároztuk, m(N)-re viszont jelenleg csak becslést tudunk adni, illetve számítógépes algoritmussal a pontos érték előállítható. Amennyiben  tehát  m(N)-re pontos értékkel rendelkezünk, akkor fennáll, hogy   

(2.28)                      =  KP(N)

 

 

 

 

 

K2.4.

 

Most a  (2.21) - (2.25)  összefüggésekből  közelítő formulát  állítunk elő, amely  K(N)-et direkt képlettel állítja elő  N-ből.  Könnyen látható, hogy 

 

(2.29)                             valamint              

Így szinte semmit nem ront a pontosságon, ha  a  (2.21) - (2.24)  összefüggésekben az összegzéseket  egységesen -ig végezzük:

 

(2.30)    K(N)=

 

 

(2.31)    Ha  a= 6u+1  és   b= 6u-1

 

              =

 

              =   

 

 

Vegyük észre, hogy     , így  K(N)-re az alábbi eredmény adódik:

 

(2.32)    

 

 

  becslésére felhasználjuk az alábbi egyenlőtlenségpárt  (Erdős-Surányi  2.old. 6.):

 

(2.33)                   

 

 

 

Alkalmazzuk  a  (2.33)  egyenlőtlenségpárt  (2.32)-re, így kapjuk hogy

 

(2.34)       

 

 

A  (2.34)  alsó és felső korlátjának számtani közepét használjuk  K(N)  közelítő értékének  (jele: KK(N) ).

 

(2.35)                                               KK(N) = 

 

 

 

 

K2.5.

 

A  (2.10) - (2.17)  levezetésekhez hasonlóan vizsgáljuk most az    (i= 1,2,3,4)   egyenlőtlenségeket, ahol    természetes szám.

 

(2.36)                

 

(2.37)              

 

(2.38)              

 

(2.39)              

 

 

Vezessük be a     (i=1,2,3,4)   jelölést, amely az összes  u,v  párok számát  jelöli, amelyek az (M,N)  intervallumba eső összes összetett számokat generálják.   Ekkor  a  (2.21) - (2.25)  összefüggések analógiájára a következőket kapjuk:

 

(2.40)                      

 

 

(2.41)                    

 

(2.42)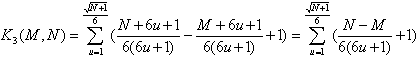                     

 

(2.43)                     

 

 

(2.44)                

 

 

Világos, hogy  az eddig levezetett  összefüggések mindegyike értelmezhető tetszőleges  (M,N)  intervallumra.  Az alábbiakban megadjuk a  (2.26), (2.27), (2.32), (2.35)  összefüggések megfelelőit tetszőleges  (M,N)  intervallumra.

 

 

(2.45)                 

 

 

(2.46)                  KP(M,N) =  

 

 (2.47)     K(M,N)=

                             =

 

 

Mivel     , így  K(M,N)-re adódik:

 

 

(2.48)    

 

 

 

 

  közelítésére felhasználjuk a (2.33)  egyenlőtlenség pár két oldalának középértékét:

 

 

 (2.49)                                KK(M,N) = 

 

 

Tehát, ha  N=6k+1 vagy  N=6k-1  alakú összetett szám, akkor   N  kéttényezős felbontásához  (2.49) szerint  maximum az alábbi lépésszám szükséges:

 

(2.50)                              

 

 

A komplementer prímszita tehát  direkt eljárást ad tetszőleges  (M,N)  intervallumban az összes összetett  (és így az intervallumba eső összes prímszám)  előállítására. Ezzel igen hatékony módszert kaptunk a prímekkel kapcsolatos három alapfeladat megoldására:

 

1. Keressük az  (M,N)  intervallumba eső  összes prímszámokat.

2. Állítsuk elő az összes prímszámokat  N-ig.  (Ekkor  M=1)

3. Állapítsuk meg egy adott   p  természetes számról, hogy prímszám-e.       

 

Nyitott probléma: az  m(N)  függvény analitikus meghatározása, vagy jó aproximációja.

 

A  3.táblázat  néhány összehasonlító értéket mutat be a fenti eredmények illusztrálására.

 

 

 

3. Táblázat    

N                          K(N)            KK(N)            m(N)         KP(N)                          KP(N)        

                                                                                                                                                              hiba %       hiba %

 


1000                      205            195                   34           162            168                        144            3.5%     14.3%

2000                      484            461                 112           294            303                        263            3.0%     13.2%

3000                      794            755                 214           420            430                        375            2.3%     12.8%

4000                    1118          1067                 325           540            552                       482            2.2%     12.7%

5000                    1452          1394                 442           656            669                       587            2.0%     12.3%

6000                    1807          1731                 577           770            783                       690            1.7%     11.8%

7000                    2160          2077                 713           886            900                       791            1.5%     12.1%

8000                    2532          2431                 857           991          1007                      890            1.5%     11.6%

9000                    2905          2792               1006         1101          1117                     988            1.4%     11.5%

10000                  3281          3159               1160         1212          1229                  1086            1.4%      11.6%

11000                  3666          3531               1316         1316          1335                  1182            1.4%      11.5%

12000                  4055          3909               1474         1419          1438                  1278            1.3%      11.1%

13000                  4454          4291               1648         1527          1547                  1372            1.3%      11.3%

14000                  4850          4677               1815         1631          1652                  1466            1.2%      11.3%

30000                11641        11266               4891         3250          3245                 2910            0.2%      10.3%   

50000                20796        20175               9263         5133          5133                 4621            0.0%      10.0%

70000                30409        29537             14013         6937          6935                 6275            0.0%        9.5%

90000                40335        39220             19053         8718          8713                 7890            0.0%        9.4%

190000               92971        90619             46813       17175        17170             15632            0.0%       8.9%

350000             183080      178739             96357       29943        29977            27417            0.1%       8.5%

900000             517786      506647          289266       71480         71274            65645             0.1%       7.9% 

1000000           581158      568777          326493       78668         78498            72382             0.2%       7.8%

1500000           905437      886863          520366     114929       114155          105478              0.6%      7.6%

2000000         1239132    1214375          721684     149218       148933         137849             0.2%       7.4%

3000000         1926146    1889011        1143113     216967       216818         201152             0.6%       7.2%

4000000         2632033    2582508        1581846     283146       283148         263127             0.0%       7.0%

5000000         3351917    3290031        2033930     348679       348515         324150             0.4%       7.0%

6000000         4083022    4008733        2495735     412713       412851         384436             0.3%       6.9%

7000000         4823413    4736732        2966794     476714       476650         444122             0.1%       6.8%

8000000         5571739    5472690        3445726     540653       539779         503304             0.1%       6.7%

10000000       7088528    6964708        4416529     661334       664579         620421             0.4%       6.6%

 

 

 

 

 

 

 

Irodalomjegyzék

 

 

[1]  Erdős Pál,  Surányi János:  Válogatott fejezetek a számelméletből

                                                         Polygon, Szeged, 1996.

 

 

[2]  H.Halberstam, K.F.Roth: SEQUENCES

                                               IV. Sieve methods

                                               Oxford at the Clarendon Press, 1966

 

[3]  K.Ramachandra:  Many famous conjectures on primes

                                   Meagre but precious progress of a deep nature

                                   The Mathematics Student, Vol. 67, 1-4 (1998), 187-199

 

[4]  A.V. Spivak:  The Sieve of Eratosthenes and Wallis's Product:

                            How Two Wrong Arguments Give One Correct Answer

                            The Mathematical Intelligencer, 23(2001) 64-65